Mathematics at Davyhulme
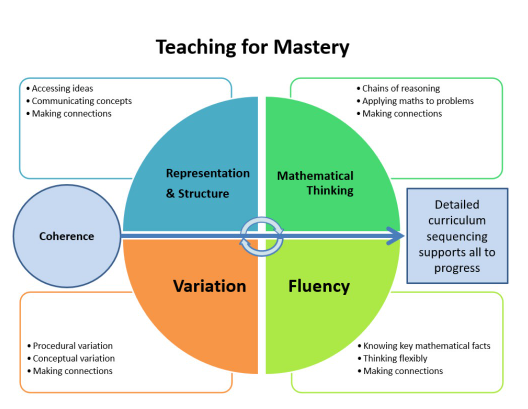
At Davyhulme Primary School we teach Mathematics using the mastery approach. Over several years our school has been a part of the North West NCETM Maths hub which has led to a deep and sustainable understanding of maths for staff and pupils.
Intent
Our school encourages a culture of mathematical thinking to deepen understanding, confidence and competence in maths – a culture that produces strong, secure learning and real progress. Research has shown that children’s chances of success are maximised if they develop deep and lasting understanding of mathematical procedures and concepts.
Implementation
The mastery approach places an emphasis on fluency of essential skills and the whole class having a deep understanding of a concept before moving on to the next small step.
The key features of mastery
- The classwork together on the same topic.This does not mean that some children will be left behind or others not challenged. Differentiation is now achieved through intervention and deeper understanding;
- Teacher intervention to prevent gaps- Those children that have not met the expected outcomes or have gaps in their understanding, will be helped by receiving short, immediate extra time on maths later in the day. This is a positive opportunity to consolidate their understanding;
- Challenge provided by going deeper not accelerating. For those children that have mastered the skill, concept or procedure they will be presented with higher-order thinking activities, rather than accelerating through the curriculum;
- Focused, rigorous and thorough teaching. The idea is to focus on one small step at a time in a lesson, with an emphasis on the mathematical structures involved and the best way to represent these through models and images. Each small step is important as it builds towards deep understanding of a concept;
- More time on teaching topics – depth and practice. The same topic is likely to have the same focus until the class has mastered the concept, skill or procedure being taught. This is particularly the case for number and calculations. Although the focus areas are being taught over a longer time, there are smaller steps of progress and the extra time is for practice and depth, making the learning effective.
For our long term and medium-term planning we use White Rose Maths. We do not follow this as a ‘scheme’. As reflective practitioners we also incorporate some elements of the NCETM curriculum prioritisation materials, and other carefully selected resources to provide the best pupil outcomes. Each lesson follows a small steps plan, and always has an element of greater depth challenge.
Reasoning and problem solving
We incorporate reasoning and problem solving throughout our lessons. This is taught using resources from I See Maths and also NCETM and NRich materials. We use a set of routines within interactive teaching which ensure mass participation within the lessons. Using these routines allows time for children to process their thinking, raising their internal narrative, and gives opportunity to free up their working memory. Normalising these routines means that the children know their importance. (Please see the Culture of mathematical thinking document for further information).
Differentiation
The Mastery approach is based upon the belief that all children can achieve. At Davyhulme Primary differentiation is provided through the support of the less able, with fluency taught through essential practice and consolidation tasks, teaching conceptual understanding through multiple representations and dealing with misconceptions immediately.
Those pupils who have achieved fluency can move on to the application of skills in different contexts. More able learners are challenged through higher-order questioning and rich tasks that develop problem-solving and reasoning skills. No one moves onto a higher year groups objectives, everyone is working on the same concept, and it is possible to provide whole class lessons but with different levels of support and challenge.
For example, when learning about multiplication having a competent knowledge of multiplication is just the beginning as children are challenged by representing multiplication in different ways – using concrete, pictorial and then moving to symbolic representations. Pupils are then encouraged to be able to make connections to repeated addition, use arrays, link to division and use accurate vocabulary to explain and reason about their work. Real-life word problems are used to provide context and purpose for learning. Similarly is the application to puzzles, problems and investigations to promote deeper mathematical thinking.
Mastering Number
EYFS and Key Stage One follow the Mastering Number programme in addition to the maths lessons. This supports children to develop good number sense in Reception through to Year 1 and Year 2. The aim over time is that children will leave KS1 with fluency in calculation and a confidence and flexibility with number. Attention is given to key knowledge and understanding needed in Reception classes, and progression through KS1 to support success in the future. This year the school is offering Mastering Number at Home family workshops to support pupils at home.
Impact
- Children accept the ‘challenge of mathematics’ because they are encouraged by the belief that everyone can succeed through effort.
- Children demonstrate their growing understanding of mathematics through their reasoning and willingness to explain their mathematical strategies.
- Children develop their mathematical language and vocabulary to widen their access and enjoyment of Maths.
- Children recognise that physical and verbal representations of mathematical ideas are as valuable as written ones.
What the children say:
We value the opinions of our children. Children from across Key Stage One and Two were able to share their thoughts about their learning.
In Key Stage 1 the children talked about what they liked learning about in the lessons:
“I like to find odd and even numbers”
“I like writing number sentences. Some are hard, but when I learn it is easy.”
“I liked learning about money because now I can buy things!”
“I liked using part whole models. There were so many missing numbers!”
“I liked column addition because some of the numbers were really big numbers!”
“I ordered numbers. I knew 9 was the smallest because it only has one digit.”
The children were asked what helps them to learn in Maths lessons. They said:
We use number lines, number strips, cubes and counters.
We work on the carpet together.
We do work with a partner or as a table group.
My teacher and teaching assistant help me.
The children all believed they have improved their understanding of Maths this year. Some comments were:
“I have learned to write my 2s instead of them looking like a 5. Now it looks like a real 2!”
“I am a lot faster, and a lot smarter!”
The lessons “help me learn, even if I get things wrong.”
In Key Stage 2 all the children said:
- They enjoy the Maths lessons.
- They all strongly agreed that they are proud of the work that they produce in their lessons.
- They all said that they want to do well in Mathematics.
- The children all agreed that they are able to use what they have learned outside of school.
The children were all clear about how to improve their understanding. Comments included:
“The teacher explains things clearly in the lessons.”
“I am able to choose some of my activities.”
“I use bar models to help me to understand a question.”
“The teacher explains things slowly and carefully.”
“We check our work, and if we are struggling, the teacher will go over it with us.”
The children identified some aspects of Mathematics at Davyhulme that they enjoy. These included:
- Times Table Rockstars
- Learning with Parents activities
- Daily 10 arithmetic challenges
- Being able to use technology to support their learning.
- Games which the teachers play to help us to learn multiplication and division.
Curriculum Overview
| Culture of Mathematical Habits at DPS (5th Jul 2023) | Download |
| Stem sentences and how we use them (2nd Mar 2023) | Download |
Year Group Overviews
| Year 6 Overview (24th Nov 2023) | Download |
| Year 5 Overview (24th Nov 2023) | Download |
| Year 4 Overview (24th Nov 2023) | Download |
| Year 3 Overview (24th Nov 2023) | Download |
| Year 2 Overview (24th Nov 2023) | Download |
| Year 1 Overview (24th Nov 2023) | Download |
Small Steps in Learning Year 1
| Summer Year 1 (24th Nov 2023) | Download |
| Spring Year 1 (24th Nov 2023) | Download |
| Autumn Year 1 (24th Nov 2023) | Download |
Small Steps Year 2
| Summer Year 2 (24th Nov 2023) | Download |
| Spring Year 2 (24th Nov 2023) | Download |
| Autumn Year 2 (24th Nov 2023) | Download |
Small Steps Year 3
| Year 3 Summer (4th Dec 2023) | Download |
| Year 3 Spring (4th Dec 2023) | Download |
| Year 3 Autumn (4th Dec 2023) | Download |
Small Steps Year 4
| Year 4 Summer (4th Dec 2023) | Download |
| Year 4 Spring (4th Dec 2023) | Download |
| Year 4 Autumn (4th Dec 2023) | Download |
Year 5 Small Steps
| Year 5 Summer (4th Dec 2023) | Download |
| Year 5 Spring (4th Dec 2023) | Download |
| Year 5 Autumn (4th Dec 2023) | Download |
Year 6 Small Steps
| Year 6 Summer (4th Dec 2023) | Download |
| Year 6 Spring (4th Dec 2023) | Download |
| Year 6 Autumn (4th Dec 2023) | Download |
Davyhulme Primary School, Canterbury Road, Davyhulme, Manchester M41 0RX Phone: 0161 748 3392
 Menu
Menu

